DSolve[{x[t] == y[t], y[t] == -a2x[t], x[0]==l,y[0]==0}, {x[t],y[t]},t]

{{xM

p-Iat plat J J

В примере мы воспользовались встроенной функцией. Если необходимо нарисовать графики полученных решений или фазовый портрет динамической системы, то второй аргумент у функции DSolve следует задать в следующем виде:

sol2 = DSolve[{x[t] == y[t],y[t] == -a-2x[t], x[0]==l,y[0] 0},{x,y},{t}]

{x -> Function[t, ----1--],

Последний ответ представлен с помощью так называемых чистых функций, с которыми можно будет познакомиться позднее. Сейчас мы просто воспользуемся этим результатом для того, чтобы нарисовать графики функций хЩ и y[i\ (рис. 2.3).

Plot[Evaluate[{x[t],y[t]} /. sol2 /. а1/2], {t,-2Pi,2Pi}]

Фазовый портрет можно нарисовать с помощью функции ParametricPlot (рис. 2.4):

ParametricPlot[Evaluate[{x[t],y[t]} /. sol2 /. а-> 1/2], {t,-2Pi,2Pi}, AspectRatio Automatic]

Рис. 2.4

Даже усиленная версия функции DSolve не может найти символьных решений всех обыкновенных дифференциальных уравнений. Встроенной функцией „Математики", реализующей один из численных методов решения обыкновенных дифференциальных уравнений, является функция ND-Solve. Проанализируем, используя NDSolve, нелинейные колебания системы, параметры которой изменяются со временем. Пусть система описывается уравнениями: x{t) = y{t), y{t) = -x{t) - 0.7cos(0.3f)sini(f). Поставим начальные условия z(0) = 1, j/(0) = О и вычислим выражение:

nlosc = NDSolve[{x[t] == y[t],

y[t] == -x[t] - 0.7Cos[0.3t]Sin[x[t]],

x[0] == l,y[0] == 0},{x,y},{t,0,3Pi}]

{{i InterpolatingFunction[{0,9.4247S},<>],

у InterpolatingFunction[{0,9.42478}, <>]}}

Результатом вычисления являются две интерполяционные функции для x{t) н y{t) на интервале (0,9.42478). С их

помощью можно вычислить значения решения в любой точке этого интервала:

{х[1],у[1]} /. nlosc {{0.299012,-1.21722}}

или нарисовать фазовый портрет колебаний (рис. 2.5):

ParametricPlot[Evaluate[{x[t],y[t]} /. nlosc],{t,0,3Pi}, AspectRatio -> Automatic]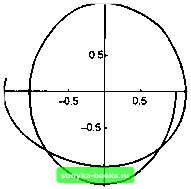

Рис. 2.5

Еще один способ получения приближенных решений, но уже в символьной форме - это метод рядов. Найдем приближенное ограниченное решение дифференциального уравнения ху{х) - y(i)2 - I = о в окрестности особой точки а; = О в виде отрезка степенного ряда с точностью 0[а:]. Задача сводится к определению семи коэффициентов в формуле у{х) = ао +aix + ... + абХ+ 0[ху. Поскольку решение ищется в виде отрезка ряда, определим объект:

у[х ] := SeriesData[x,0, Аггау[а,7,0]]

Обратим внимание на два обстоятельства. Во-первых, мы использовали так называемое отложенное определение, поэтому